Diese Seite funktioniert nur mit Javascript.
Der Grenznutzen2.2.2.1 Grenznutzen und UnsicherheitIndifferenzkurven
Die Taube auf dem Dach ... oder den Spatz in Hand?
Dieser Exkurs behandelt fortgeschrittene Fragestellungen. Sie können ihn überspringen, wenn Sie sich nicht für das Thema Unsicherheit interessieren. Für das Verständnis ist es von Vorteil, wenn Sie mit dem Begriff Erwartungswert umgehen können und mit den Spielregeln der Quizsendung "Wer wird Millionär?" vertraut sind.
Nur selten meistert ein Kandidat in der Quizshow "Wer wird Millionär?" (WWM) die 125.000-Euro-Frage. Wenn wir ein solches Ereignis aber am Bildschirm verfolgen können, dann wird es nicht nur spannend, sondern die Situation bietet ein schönes Anwendungsbeispiel für unsere Grenznutzenüberlegungen. Spannend wird es vor allem deswegen, weil sich der Gewinnbetrag an dieser Stelle nicht wie sonst in dieser Quizshow verdoppelt, sondern vervierfacht. Die richtige Beantwortung der nächsten Frage wird mit 500.000 Euro belohnt.
Nennen wir unseren Kandidaten K. Er soll noch über den 50:50-Joker verfügen, als der Moderator ihm die 500.000-Euro-Frage stellt: "Bei wem handelt es sich um einen Ökonomen?"
|
A |
Ailton |
B |
Elber |
|
C |
Amoroso |
D |
Pizarro |
K. ist sich nicht sicher - um nicht zu sagen, er hat keinen blassen Schimmer - und setzt den 50:50-Joker:
|
A |
Ailton |
B |
|
|
C |
Amoroso |
D |
|
Glück gehabt, denn K. hätte auf Pizarro getippt. Sie auch? Nun ist guter Rat teuer, denn K. hält die beiden verbliebenen Antworten A und C für gleich wahrscheinlich. Jetzt heißt es, einen kühlen Kopf zu bewahren. Da K. im Moment viel zu aufgeregt ist, nehmen wir ihm die Analyse der Situation ab.
Wenn K. falsch antwortet, so fällt er auf einen garantierten Gewinnbetrag von 16.000 Euro zurück. Wenn K. richtig antwortet, dann könnte er mit einem Gewinn von 500.000 Euro das Spiel beenden. Wir wollen an dieser Stelle noch annehmen, dass er das Spiel dann auch tatsächlich beenden würde, da wir ansonsten natürlich noch den Wert der Chance, um die Million spielen zu können, in unsere Analyse einbeziehen müssten.
Mit den beiden Gewinnbeträgen und dem Wissen, dass beide Ereignisse mit gleicher Wahrscheinlichkeit eintreten, weil K. raten müsste, können wir einen dritten Betrag berechnen, der praktisch gar nicht zustande kommen kann:
$$E = 0.5 \cdot 16.000 + 0.5 \cdot 500.000 = 258.000 \tag{1}$$Hierbei handelt es sich um den "erwarteten Gewinn" $E$. Dieser Betrag wäre ein "fairer Preis" oder fairer Einsatz für das Spiel, wenn man es wieder und wieder spielen könnte. Auf die Dauer würden sich Einsatz und Gewinnsumme die Waage halten.
Im nächsten Schritt wollen wir darüber nachdenken, welchen Preis K. für das Spiel zahlen muss. Er könnte im Moment mit einer Gewinnsumme von 125.000 Euro das Spiel beenden. Dieser Betrag ist sein Spieleinsatz, denn er müsste auf diese Alternative verzichten, um das Spiel zu spielen. K. ist also in einer Situation, in der er sich darüber klar werden muss, ob er für ein Spiel, das im Durchschnitt 258.000 Euro wert ist, einen Einsatz von 125.000 aufbringen möchte.
Na klar, könnte man jetzt sagen: das wird er auf jeden Fall machen. Er kann ja quasi 258.000 Euro für 125.000 Euro kaufen (von den Euro, auf die er zurückfallen würde, sehen wir ab). So ein Geschäft bietet sich nicht jeden Tag!
Doch so einfach ist die Überlegung nicht, denn die 258.000 Euro werden ja nur im Durchschnitt, nicht aber tatsächlich ausgezahlt. Der Fehler wäre also, dass man Äpfel und Birnen vergleichen würde. Die Taube auf dem Dach ist ja auch nicht besser als der Spatz in der Hand.
Die entscheidende Frage lautet: übertrifft der Nutzen, den K. aus dem Spiel erwarten kann, die Kosten (Nutzenverlust), die durch den Einsatz entstehen? Erst wenn wir wissen, ob K. aus dem Spiel einen höheren Nutzen erwartet als aus dem aufzubringenden Einsatz, können wir sagen, ob er eine Antwort riskieren wird oder nicht.
Wenn wir beobachten würden, dass er keine Antwort wagt, könnten wir ohne weitere Informationen etwas über K's Risikobereitschaft aussagen. Da der erwartete Gewinn über dem Einsatz liegt, dürfen wir K. risikoscheu oder risikoavers nennen. Mit anderen Worten: K. müsste für dieses Spiel weniger als den fairen Einsatz zahlen. Er würde uns somit durch einen Spielverzicht deutlich signalisieren, dass er das Risiko scheut.
Um uns dem letzten Analyseschritt zuzuwenden, treffen wir noch zwei weitere Annahmen, die wir aber später leicht modifizieren können und die von daher die Qualität der noch abzuleitenden Ergebnisse nicht beeinträchtigen. Erstens sei angenommen, dass K. zurzeit über kein Vermögen verfügt. In wenigen Augenblicken werden wir das Gegenteil unterstellen und davon ausgehen, dass K. ein vermögender Mann ist. Zweitens sei angenommen, K's Nutzenfunktion laute
$$U = \sqrt G = {G^{0,5}} \tag{2}$$wobei $G$ das in Geldeinheiten gemessene Vermögen von K. anzeigt. Die Nutzenfunktion (2) ist mit den markanten Werten in Abbildung 1 dargestellt.
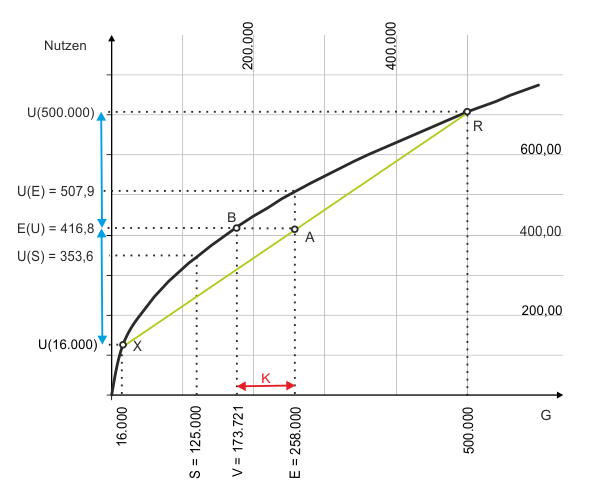
Zunächst informiert uns die maßstabsgetreue grafische Darstellung, dass K's Grenznutzen aus Geldvermögen abnimmt, da die Steigung der Nutzenfunktion abnimmt. Analytisch bestätigt sich die Gültigkeit des ersten Gossenschen Gesetzes durch
$$U' = 0,5{G^{ - 0,5}} > 0 \tag{3}$$ $$U'' = - 0,25{G^{ - 1,5}} \lt 0 \tag{4}$$Die grüne Gerade XR, die den Nutzen des garantierten Gewinns in Höhe von 16.000 Euro und den Nutzen des Gewinns in Höhe von 500.000 Euro verbindet, nutzen wir zur grafischen Ermittlung zweier Mittelwerte (Punkt A). Erstens liegt auf genau halber Strecke die oben berechnete erwartete Gewinnsumme E von 258.000 Euro. Zweitens können wir an der Nutzenachse ablesen, welchen Nutzen E(U) K. erwarten kann:
$$E(U) = \left( {1 - p} \right) \cdot U(16.000) + p \cdot U(500.000) \tag{5}$$Dabei ist $p$ die Wahrscheinlichkeit, richtig zu antworten, die uns mit 0,5 bekannt ist. Also können wir
$$E(U) = \left( {1 - 0.5} \right) \cdot 126,5 + p \cdot 707,1 = 416,8 \tag{6}$$berechnen. Der (erwartete) Wert des Spiels in Nutzeneinheiten beträgt also 416,8 Einheiten. Diesen Nutzen könnte K. aber auch dann erreichen (Punkt B in Abb. 1), wenn er ein Vermögen
$${416,8^2} = 173.721,36 \tag{7}$$sicher hätte, denn dieser Betrag stiftet ja gerade einen Nutzen in Höhe von 416,8.
Die berechnete Geldsumme heißt Sicherheitsäquivalent. K. wäre gerade indifferent, wenn er zwischen dem Sicherheitsäquivalent und dem Spiel wählen sollte.
Der Nutzen des Einsatzes ist mit
$$U(S) = U(125.000) = 353,6 \lt U(E)\tag{8}$$deutlich geringer als der erwartete Nutzen aus dem Spiel, sodass wir die Kernfrage beantworten können: K. wird eine Antwort wagen. Ebenso hätten wir auch prüfen können, ob der Spieleinsatz geringer als das Sicherheitsäquivalent ist, und wären - da sich das natürlich bestätigt - zum gleichen Resultat gekommen.
Mit den berechneten Werten können wir noch eine weitere interessante Überlegung anschließen: Ziehen wir vom erwarteten Gewinn des Spielers $E$ das Sicherheitsäquivalent ab, so erhalten wir die Kosten des Risikos, die auch Risikoprämie genannt werden:
$$K = 258.000 - 173.721,36 = 84.278,64 \tag{9}$$Warum macht es Sinn, diesen Betrag die "Kosten des Risikos" zu nennen? Der faire Preis für das Spiel wäre 258.000 Euro. K. wäre für einen Betrag von 173.721,36 Euro aber gerade so eben zum Verkauf des Spiels bereit. Er würde es sich also 84.278,64 Euro kosten lassen, das Risiko zu vermeiden.
- Wenn die beschriebene Spielsituation sehr häufig auftreten würde, hätten Sie vielleicht eine Geschäftsidee, die irgendwie an "Glaspaläste" erinnert?
- Ein Individuum habe
die Nutzenfunktion \(U=\sqrt{G}\). Vergleichen
Sie hinsichtlich der subjektiven Kosten des Risikos
die Situation A, dass die beiden Ereignisse \(G=100\)
und \(G=900\) mit je einer Wahrscheinlichkeit von \(p=0,5\)
eintreten, mit der Situation B, dass die Ereignisse
\(G=0\) und \(G=1.600\) mit denselben Wahrscheinlichkeiten
eintreten!
Können Sie eine plausible Erklärung für Ihr Ergebnis anbieten? - Zahlreiche identische
Individuen haben die Nutzenfunktion \(U=\sqrt{G}\).
Mit gleicher Wahrscheinlichkeit treten die Ereignisse
\(G=100\) bzw. \(G=900\) ein.
Zeigen Sie, dass es sich sowohl für eine Versicherung als auch für die Individuen rechnet, eine Versicherung zum Preis von 420 Euro abzuschließen, die im Schadenfall das Einkommen von 100 auf 900 Euro aufstockt!
- Wie hoch ist der durchschnittliche
Profit der Versicherung je Vertrag?
- Wie hoch ist
der Reservationspreis der Individuen für die
Versicherung?
- Warum wird im Unterschied zu diesem
Rechenbeispiel eine Versicherung den Schaden i.d.R.
nicht voll ersetzen?
Dass unser Kandidat risikoavers ist, erkennen wir auch daran, dass $U(E)$ größer als $E(U)$ ist (s. Abbildung 1). Diese Erkenntnis wird auch typischerweise benutzt, um Risikoscheu zu definieren: Wenn der Nutzen des Erwartungswertes den erwarteten Nutzen übersteigt, zieht der Spieler das sichere dem unsicheren Ergebnis vor.
Schlechtere Chancen ohne 50-50-Joker
Für ein zweites Zahlenbeispiel sei angenommen, K. verfüge nicht mehr über den 50-50-Joker. Wenn alle weiteren Annahmen beibehalten werden, können wir zunächst den erwarten Gewinn berechnen. Dabei ist im Unterschied zu Gleichung (5) nur zu beachten, dass die Wahrscheinlichkeit, richtig zu raten, auf 25 % sinkt:
$$E = 0,75 \cdot 16.000 + 0,25 \cdot 500.000 = 137.000 \tag{10}$$Der erwartete Nutzen beträgt
$$E = 0,75 \cdot U(16.000) + 0,25 \cdot U(500.000) = 271,65 \tag{11}$$Der Einsatz hingegen bleibt unverändert, sodass der in (8) berechnete Nutzenverlust aus dem Einsatz 353,6 den Wert des Spiels nun nicht mehr aufwiegt. K. würde ohne 50-50-Joker also keine Antwort riskieren. Das können Sie auch daran erkennen, dass das Sicherheitsäquivalent nun nur noch 73.791,02 Euro beträgt.
Risikoneigung und Vermögen
In der am 6.4.02 ausgestrahlten WWM-Sendung schwankte ein Kandidat, der die Frage nach seiner beruflichen Tätigkeit mit "Beamter im niedersächsischen Kultusministerium" beantwortet hatte, bei einem nicht unerheblichen Betrag zwischen Aufhören und Weiterspielen. Der Moderator der Sendung, Günter Jauch - an spannender Unterhaltung interessiert, die sich besonders bei höheren Beträgen einstellt und hohe Einschaltquoten verspricht - ermunterte den Kandidaten mit den Worten (sinngemäß): "Na, sie sind doch Beamter auf Lebenszeit." Die weiteren nicht gesprochenen Worte, die sich jeder denken konnten, lauteten natürlich: "Da können sie es sich doch leisten".
In unser Ökonomendeutsch übersetzt heißt das, dass für einen Lebenszeitbeamten die Kosten des Risikos geringer sind als für einen "Durchschnittsverdiener". Nehmen wir an, es entspricht den Tatsachen, dass Beamte überdurchschnittlich gut verdienen und der Kandidat über ein nicht unerhebliches Vermögen verfügt. Wiederum modifizieren wir eine Annahme im Vergleich zum vorausgegangenen Beispiel und unterstellen, der Kandidat verfügt gegenwärtig über ein Vermögen in Höhe von 1.000.000 Euro - ist also Euro-Millionär.
Der erwartete Nutzen aus dem Vermögen wäre nun bei der Entscheidung für das Spiel
$$E = 0,75 \cdot U(1.000.000 + 16.000) + 0,25 \cdot U(1.000.000 + 500.000) = 1.062,16 \tag{12}$$Wenn der Kandidat nicht spielen würde, könnte er über 1.000.000 Euro eigenes Vermögen plus seinen sicheren Gewinn in Höhe von 125.000 Euro verfügen, sodass sein Nutzen
$$U(1.000.000 + 125.000) = 1.060,66 \tag{13}$$betrüge. Die Entscheidung würde tatsächlich zugunsten des Spiels kippen. Allerdings mussten wir dazu - das Ergebnis ist ja denkbar knapp - den Kandidaten "ganz schön reich" machen.
Das sichere Äquivalent zum in (12) bestimmten Nutzen wäre ein Betrag von 1.128.188,98 Euro. Da der Kandidat 1.000.000 Euro Vermögen besitzt, wäre er gerade so bereit, das Spiel für 128.188,98 Euro zu verkaufen. Damit ist das Spiel für ihn wertvoller als der Einsatz in Höhe von 125.000 Euro. Er wird also spielen.
Das erwartete Vermögen betrüge in diesem Fall
$$E = 0,75 \cdot (1.000.000 + 16.000) + 0,25 \cdot (1.000.000 + 500.000) = 1.137.000 \tag{14}$$Die Kosten des Risikos wären demnach $1.137.000-1.128.188,98 = 8.811,02$ Euro. Wie vermutet, sinken die Kosten des Risikos mit dem Vermögen des Spielers.
-
Ein Individuum habe
die Nutzenfunktion \(U=G^2\) und stehe vor der Entscheidung,
ein Münzwurfspiel, das zum fairen Preis angeboten
wird, zu spielen. Fällt "Adler" gewinnt
er einen Euro, fällt Zahl, geht er leer aus.
Analysieren Sie das Spiel mithilfe einer Skizze. Ist das Individuum risikofreudig oder risikoavers? Welchen Wert müsste der Exponent in der Nutzenfunktion annehmen, damit die Kosten des Risikos verschwinden? - Was meint die Aussage, Lottospieler zahlten Dummensteuer? Wie ist diese Behauptung vor dem Hintergrund der Erläuterungen in diesem Exkurs einzuschätzen?
Nach ähnlichen Seiten im WWW suchen
